Výpočtové modelování konstrukcí podkroví

Úvodem

Při tepelně technickém posouzení šikmých střech a dalších konstrukcí vestavěného podkroví je třeba obvykle vyřešit několik specifických problémů počínaje vlivem opakujících se tepelných mostů ve skladbě konstrukce a konče například vlivem mechanického upevnění parozábrany. Řada projektantů však bohužel tyto nepříznivé vlivy ve výpočtech stále nezohledňuje a posuzuje tak ve skutečnosti poněkud jiné konstrukce – bez tepelných mostů a daleko těsnější – což pak následně může vést i k malým bezpečnostním rezervám v jejich návrzích. Korektní modelování konstrukcí vestavěných podkroví přitom není zas tak obtížné – stačí dodržovat některá základní pravidla.

Podívejme se nejprve na možnosti výpočtu součinitele prostupu tepla šikmých střech s tepelnou izolací a podobných konstrukcí s opakujícími se (systematickými) tepelnými mosty.

Výpočet součinitele prostupu tepla

Jakmile se v konstrukci v pravidelných osových vzdálenostech opakují určité tepelné mosty (tj. mají systematický charakter), je naprosto nezbytné zahrnout jejich vliv do celkových tepelně izolačních vlastností konstrukce. Jednoznačně to požaduje i ČSN 730540-2 – je proto hrubou chybou tento vliv zanedbat a počítat součinitel prostupu tepla v některém z „typických“ či „ideálních“ řezů (např. v místě mezi krokvemi). Chyba vzniklá tímto postupem se snadno může pohybovat i v řádu desítek procent, což pak nezřídka vede k tomu, že projektant navrhne bez váhání skladbu, která nesplňuje požadavky ČSN 730540-2 na součinitel prostupu tepla.

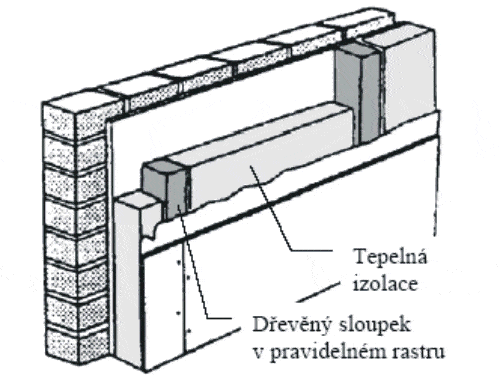
Obr.1   Příklad konstrukce se systematickými tepelnými mosty dle [1]

Tepelné mosty je přitom možné alespoň orientačně zohlednit velmi snadno. Při prvních odhadech a návrzích konstrukce obvykle postačuje upravit tepelnou vodivost rozhodující tepelně izolační vrstvy, v níž jsou umístěny tepelné mosty (Obr. 1). Použít lze například vážený průměr přes průřezové plochy

      (1)

kde λ_i je tepelná vodivost i-tého materiálu ve W/(m.K) a A_i je plocha i-tého materiálu v m². Obě veličiny se uvažují ve vztahu k řezu konstrukcí (Obr. 2).

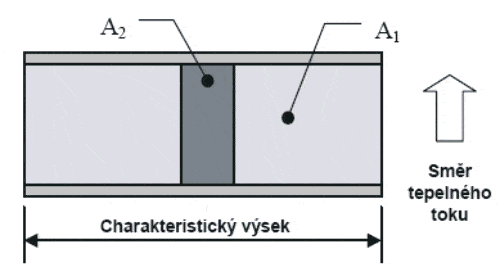
Obr. 2   Charakteristický výsek lehké konstrukce a dílčí plochy

Variantně lze použít i orientační postup doporučovaný J. Šálou [2]

       (2)

kde λ_z je tepelná vodivost tepelné izolace bez vlivu mostů ve W/(m.K) a Z je činitel tepelných mostů, který lze podle [2] uvažovat Z=1,1 pro šikmé střechy s tepelnou izolací nad či pod krokvemi, Z=1,25 pro šikmé střechy s tepelnou izolací mezi krokvemi a pod či nad nimi a konečně Z=1,40 pro šikmé střechy s tepelnou izolací jen mezi krokvemi.

Už z těchto orientačních výpočtů je zřejmé, že vliv tepelných mostů může znamenat zhoršení tepelné vodivosti rozhodující tepelně izolační vrstvy hrubým odhadem až o 40%. Podívejme se nyní na přesnější postup výpočtu součinitele prostupu tepla, který je již vhodný i pro ověření návrhu šikmých střech a dalších obdobných konstrukcí ve vytápěných podkrovích.

Zmíněný postup je sice definován v ČSN EN ISO 6946 jako přibližný, nicméně pro hodnocení konstrukcí s dřevěnými tepelnými mosty poskytuje dosti přesné výsledky (málo přesný je hlavně pro tepelné mosty tvořené kovovými prvky). Prvním krokem tohoto výpočtu je rozdělení charakteristického výseku konstrukce s tepelným mostem na dílčí části podle schématu na Obr. 3.

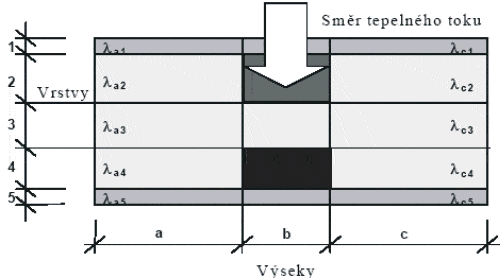
Obr. 3   Rozdělení výseku konstrukce na části

Součinitel prostupu tepla včetně vlivu tepelného mostu lze pak stanovit jako

       (3)

kde R’_T je horní mez a R’’_T dolní mez tepelného odporu při prostupu tepla v m².K/W. Hodnotu R’_T lze stanovit ze vztahu

     (4)

kde f_a až f_q jsou poměrné plochy dílčích výseků hodnocené konstrukce a R_Ta až R_Tq jsou tepelné odpory při prostupu tepla v m².K/W stanovené ve směru tepelného toku pro každý dílčí výsek. Součet všech poměrných ploch dílčích výseků musí být roven 1, přičemž poměrná plocha x-tého výseku f_x je definována jako

      (5)

kde A_x je plocha x-tého výseku v m² a A je celková plocha hodnocené konstrukce v m² (ve směru kolmém na směr tepelného toku). Hodnota R’’_T ze vztahu (3) je definovaná jako

     (6)

kde R_si a R_se jsou tepelné odpory při přestupu na vnitřní a vnější straně v m².K/W a R₁ až R_n jsou ekvivalentní tepelné odpory jednotlivých vrstev kolmých na směr tepelného toku v m².K/W. Tyto hodnoty lze určit ze vztahu

      (7)

kde R_aj až R_qj jsou tepelné odpory j-té vrstvy kolmé na směr tepelného toku ve výsecích a až q.

Přibližný způsob výpočtu je sice postupem určeným pro ruční počítání, ale na první pohled může i mírně vyděsit. Naštěstí není vždy nutné pronikat do jeho podstaty, protože existuje řada alternativních možností – např. využít vhodný software, který s tímto postupem počítá.

S vhodným programem je možné provést i nejpřesnější výpočet součinitele prostupu tepla, který vychází z řešení vícerozměrného teplotního pole (obvykle dvourozměrného) v charakteristickém výseku konstrukce. Při tomto výpočtu je velmi důležité především správné zadání geometrie charakteristického výseku a okrajových podmínek (např. tepelné odpory při přestupu tepla na vnitřní straně musí být zadány podle polohy konstrukce Rsi = 0,10/0,13/0,17 m².K/W). Jakmile je k dispozici vypočtené dvourozměrné teplotní pole v charakteristickém výseku konstrukce, lze její součinitel prostupu tepla vyjádřit ze vztahu

       (8)

kde b je šířka hodnoceného výseku v m (Obr. 2), Q je vypočtená hustota tepelného toku ve W/m, O_i a O_e jsou návrhové vnitřní a venkovní teploty ve °C a L je tepelná propustnost výsekem konstrukce ve W/(m.K). Veličiny Q a L uvádí např. program Area v protokolu o výpočtu.

Z hlediska použití programů pro tepelně technické hodnocení skladby stavební konstrukce je nutné doporučit používat jen takové z nich, které buď podporují alespoň přibližné zahrnutí vlivu tepelných mostů podle vztahů (3) až (7), nebo které umožňují alespoň hrubou orientační úpravu tepelné vodivosti podle vztahů (1) a (2).

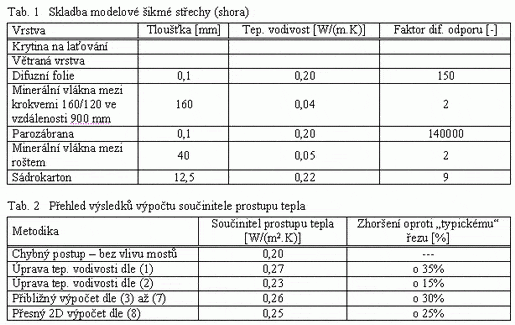
Podívejme se závěrem ještě na příklad výpočtu a srovnání výsledků jednotlivých metodik pro typickou šikmou střechu, jejíž skladba je uvedena v Tab. 1. Přehled výsledků hodnocení je uveden v Tab. 2. Z výsledků je zřejmé, že pro hodnocenou konstrukci vychází spolehlivě na straně bezpečnosti postup s použitím váženého průměru tepelné vodivosti dle vztahu (1) a také přibližný výpočet podle ČSN EN ISO 6946. Postup s použitím vztahu (2) je v tomto případě příliš „měkký“. Přesná hodnota součinitele prostupu tepla je pro uvažovanou konstrukci o 25% vyšší, než by byla hodnota stanovená pro typický řez mezi krokvemi. Prakticky to znamená, že uvažovaná konstrukce nesplňuje požadavek ČSN 730540-2 na součinitel prostupu tepla – a to právě vzhledem k vlivu tepelných mostů.

Vnitřní povrchová teplota

Z hlediska výpočtu nejnižší vnitřní povrchové teploty se obvykle nenaráží u konstrukcí vestavěných podkroví na zásadní problémy – mimo jiné i proto, že tepelné mosty tvořené dřevěnými prvky obvykle neznamenají z hlediska povrchových teplot velké riziko. Je třeba jen pečlivě zadávat do výpočtu okrajové podmínky – především tepelný odpor při přestupu tepla na vnitřní straně, který se pro tyto účely uvažuje podle ČSN 730540-2 hodnotou 0,25 m².K/W ve všech místech kromě výplní otvorů, kde zůstává jinak obvyklá hodnota 0,13 m².K/W.

Difuze vodní páry a její kondenzace

Při hodnocení difuze vodní páry konstrukcemi vestavěného podkroví se naprosto typicky zapomíná na skutečnost, že se do těchto konstrukcí parozábrany upevňují mechanicky. Nelze proto převzít faktor difuzního odporu uváděný výrobcem parozábrany a s klidným svědomím s ním provést výpočet. Ve skutečnosti bude totiž plošně zprůměrovaný faktor difuzního odporu této vrstvy vždy nižší – a to podle některých autorů až 100x [3]. Běžně se doporučuje snížit faktor difuzního odporu parozábrany na 10% laboratorně změřené hodnoty – samozřejmě za předpokladu kvalitní realizace!

Pokud by totiž byla parozábrana netěsná, nelze opravdu očekávat, že bude sebeméně plnit svou funkci. Z známých publikovaných měření [4] vyplývá, že pokud podíl plochy otvorů přesáhne 1% z celkové plochy materiálu, klesá ekvivalentní difuzní tloušťka takto poškozených vrstev vždy pod hodnotu 0,27 m, a to nezávisle na druhu materiálu. Parozábrana pak prakticky přestává jako překážka pro vodní páry fungovat.

Za zmínku stojí ještě i problematika lokální těsnosti parozábrany. Často se totiž na stavbách objeví i v jinak dobře provedené parozábraně neutěsněný prostup či netěsné napojení na okolní konstrukce. Důsledky takové lokální poruchy jsou pak také lokální a výpočtově se je s pomocí standardních normových postupů obvykle ani nepodaří postihnout. Nemusí to ovšem znamenat, že jsou zanedbatelné. Na Obr. 4 jsou pro ilustraci vidět změny v rozsahu oblasti kondenzace v již diskutované šikmé střeše – tentokrát však s lokálně netěsnou parozábranou a s lokálně netěsným sádrokartonovým obkladem (v obou případech byla uvažována spára o šířce 1 mm). Pole relativních vlhkostí platí pro exfiltraci vnitřního vzduchu přes konstrukci do exteriéru, což je z vlhkostního hlediska nebezpečnější, než infiltrace vzduchu přes konstrukci do interiéru.

Obr. 4   Relativní vlhkosti v netěsné šikmé střeše při různých tlakových gradientech

Srovná-li se těsná a netěsná modelová konstrukce při nulovém tlakovém gradientu, lze zjistit, že množství kondenzující vodní páry se vlivem netěsností zvýší na zhruba dvojnásobek (v těsné konstrukci dochází k drobné kondenzaci na spodním líci parozábrany v místech pod krokvemi). Jakmile však začne docházet i k proudění vnitřního vzduchu netěsnostmi do konstrukce, může se snadno množství kondenzátu zvýšit na 10-ti až 20-ti násobek (při tlakovém gradientu 50 Pa). Značně nepříznivý vliv netěsností je z uvedeného příkladu jasně patrný – a to jde přitom o spíše malé netěsnosti, často lze bohužel vidět daleko otřesnější případy.

Těsnost parozábrany je tedy zcela zásadní a je jí nutné věnovat velkou pozornost. V rámci modelování konstrukcí do výpočtu je pak nutné snížit její difuzní odpor, aby se ve výpočtu vytvořila bezpečnostní rezerva na případné nepřesnosti při realizaci.

Tento příspěvek byl podpořen výzkumným záměrem č. 1 MSM 210000001.

Literatura

[1] ČSN EN ISO 6946 „Stavební prvky a stavební konstrukce – Tepelný odpor a součinitel prostupu tepla – Výpočtová metoda“, 1998.
[2] J. Šála: Zateplování budov v praxi, Grada Publishing, 2004.
[3] J. Šála, K. Chaloupka: Ploché střechy a pěnový polystyren, Sdružení EPS, 2002.
[4] F. Mrlík: Difúzní konstanty některých stavebních látek a konstrukcí, VÚPS Praha – pracoviště Gottwaldov, 1980.

Ke stažení

Vzhledem k velkému množství vzorců v tomto článku, si jej můžete stáhnout ve formátu PDF v podobě, ve které byl publikován ve sborníku konference IZOLACE 2005.

Přednáška ve formátu PDF ke stažení zde.